J. Aust. Math. Soc.
81 (2006), 225-243
|
Cotorsion modules and relative pure-injectivity
|
Lixin Mao
Department of Basic Courses
Nanjing Institute of Technology
Nanjing 210013
China
and
Department of Mathematics
Nanjing University
Nanjing 210093
China
maolx2@hotmail.com
|
|
|
Nanqing Ding
Department of Mathematics
Nanjing University
Nanjing 210093, China
nqding@nju.edu.cn
|
|
|
Abstract
|
Let
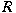 be a ring. A right be a ring. A right
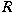 -module -module
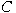 is called a cotorsion module if is called a cotorsion module if
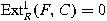 for any flat right
for any flat right
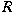 -module -module
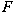 . In this paper, we first characterize those
rings satisfying the condition that every
cotorsion right (left) module is injective with
respect to a certain class of right (left)
ideals. Then we study relative pure-injective
modules and their relations with cotorsion
modules. . In this paper, we first characterize those
rings satisfying the condition that every
cotorsion right (left) module is injective with
respect to a certain class of right (left)
ideals. Then we study relative pure-injective
modules and their relations with cotorsion
modules.
|
Download the article in PDF format (size 150 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|