J. Aust. Math. Soc.
81 (2006), 425-440
|
The factorial moments of additive functions with rational argument
|
J. Siaulys
Department of Probability
Theory and Number Theory
Vilnius University
Naugarduko 24
03225 Vilnius
Lithuania
jonas.siaulys@mif.vu.lt
|
|
|
|
|
Abstract
|
We consider the weak convergence of the set of
strongly additive functions 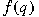 with rational argument with rational argument
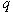 . It is assumed that . It is assumed that
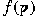 and and 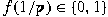 for all primes. We obtain necessary and
sufficient conditions of the convergence to the
limit distribution. The proof is based on the
method of factorial moments. Sieve results, and
Halász's and Ruzsa's inequalities are
used. We present a few examples of application of
the given results to some sets of fractions. for all primes. We obtain necessary and
sufficient conditions of the convergence to the
limit distribution. The proof is based on the
method of factorial moments. Sieve results, and
Halász's and Ruzsa's inequalities are
used. We present a few examples of application of
the given results to some sets of fractions.
|
Download the article in PDF format (size 122 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|