J. Aust. Math. Soc.  81 (2006), 369-385
C*-algebras associated with presentations of subshifts II. Ideal structure and lambda-graph subsystems

Kengo Matsumoto
  Department of Mathematical Sciences
  Yokohama City University
  Seto 22-2, Kanazawa-ku
  Yokohama 236-0027
  Japan
  kengo@yokohama-cu.ac.jp


Abstract
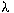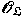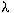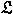A $\lambda$ -graph system is a labeled Bratteli diagram with shift transformation. It is a generalization of finite labeled graphs and presents a subshift. In Doc. Math. 7 (2002) 1–30, the author constructed a C*-algebra $\mathcal{O}_\mathfrak{L}$ associated with a $\lambda$-graph system $\mathfrak{L}$ from a graph theoretic view-point. If a $\lambda$-graph system comes from a finite labeled graph, the algebra becomes a Cuntz-Krieger algebra. 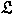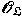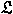In this paper, we prove that there is a bijective correspondence between the lattice of all saturated hereditary subsets of $\mathfrak{L}$ and the lattice of all ideals of the algebra $\mathcal{O}_\mathfrak{L}$, under a certain condition on $\mathfrak{L}$ called (II). As a result, the class of the C*-algebras associated with $\lambda$-graph systems under condition (II) is closed under quotients by its ideals.
Download the article in PDF format (size 169 Kb)
Australian Mathematical Publishing Association Inc. ©  Australian MS