J. Aust. Math. Soc.
81 (2006), 297–319
|
The Gelfand transform of homogeneous distributions on Heisenberg type groups
|
Francesca Astengo
Dipartimento di Matematica
Università di Genova
16146 Genova
Italia
astengo@dima.unige.it
|
|
|
|
|
Abstract
|
A distribution on a Heisenberg type group of
homogeneous dimension 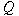 is a biradial kernel of type is a biradial kernel of type
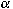 if it coincides with a biradial function,
homogeneous of degree if it coincides with a biradial function,
homogeneous of degree
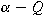 , and smooth away from the identity. We prove
that a distribution is a biradial kernel of type , and smooth away from the identity. We prove
that a distribution is a biradial kernel of type
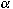 , ,
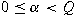 , if and only if its Gelfand transform, defined
on the Heisenberg fan, extends to a smooth even
function on the upper half plane, homogeneous of
degree , if and only if its Gelfand transform, defined
on the Heisenberg fan, extends to a smooth even
function on the upper half plane, homogeneous of
degree
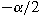 . A similar result holds for radial kernels on
the Heisenberg group. . A similar result holds for radial kernels on
the Heisenberg group.
|
Download the article in PDF format (size 166 Kb)
|
|
|
Australian Mathematical Publishing Association Inc.
|
©
Australian MS
|
|