J. Aust. Math. Soc.  81 (2006), 321-350
Filter games and pathological subgroups of a countable product of lines

Taras Banakh
  Instytut Matematyki
  Akademia Swietokrzyska
  Swietokrzyska 15
  Kielce
  Poland
  and
  Department of Mathematics
  Ivan Franko Lviv National University
  Universytetska 1
  Lviv 79000
  Ukraina
  tbanakh@franko.lviv.ua
Peter Nickolas
  School of Mathematics and
  Applied Statistics
  University of Wollongong
  Wollongong
  NSW 2522
  Australia
  peter@uow.edu.au
and
Manuel Sanchis
  Departament de Matemàtiques
  Universitat Jaume I
  Campus de Penyeta Roja
  s/n 12071
  Castellón
  Spain
  sanchis@mat.uji.es


Abstract
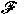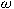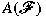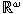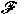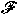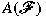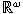To each filter $\mathcal{F}$ on $\omega$, a certain linear subalgebra $A(\mathcal{F})$ of $\mathbb{R}^{\omega}$, the countable product of lines, is assigned. This algebra is shown to have many interesting topological properties, depending on the properties of the filter $\mathcal{F}$. 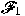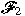For example, if $\mathcal{F}$ is a free ultrafilter, then $A(\mathcal{F})$ is a Baire subalgebra of $\mathbb{R}^{\omega}$ for which the game OF introduced by Tkachenko is undetermined (this resolves a problem of Hernández, Robbie and Tkachenko); and if $\mathcal{F}_1$ and $\mathcal{F}_2$ are two free filters on 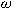$\omega$ that are not near coherent (such filters exist under Martin's Axiom), then 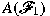$A(\mathcal{F}_1)$ and $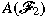A(\mathcal{F}_2)$ are two o-bounded and OF-undetermined subalgebras of $\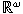mathbb{R}^{\omega}$ whose product $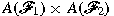A(\mathcal{F}_1)\times A(\mathcal{F}_2)$ is OF-determined and not o-bounded (this resolves a problem of Tkachenko). 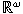It is also shown that the statement that the product of two o-bounded subrings of $\mathbb{R}^{\omega}$ is o-bounded is equivalent to the set-theoretic principle NCF (Near Coherence of Filters); this suggests that Tkachenko's question on the productivity of the class of o-bounded topological groups may be undecidable in ZFC.
Download the article in PDF format (size 275 Kb)
Australian Mathematical Publishing Association Inc. ©  Australian MS