Suppose
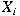 , ,
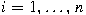 are independent and identically distributed
with are independent and identically distributed
with 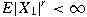 , ,
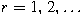 . If . If
 for
for
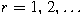 , where , where
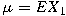 , ,
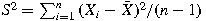 , and , and
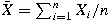 , then we show that , then we show that
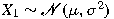 , where , where
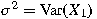 . This
covariance zero condition characterizes
the normal distribution. It is a moment
analogue, by an elementary approach, of the
classical characterization of the normal
distribution by independence of . This
covariance zero condition characterizes
the normal distribution. It is a moment
analogue, by an elementary approach, of the
classical characterization of the normal
distribution by independence of
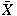 and
and
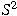 using semi-invariants. More generally, if
Cov
using semi-invariants. More generally, if
Cov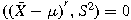 for
for
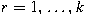 , then , then
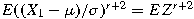 for
for
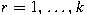 , where , where
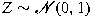 . Conversely . Conversely
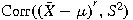 may be arbitrarily close to unity in absolute
value, but for unimodal
may be arbitrarily close to unity in absolute
value, but for unimodal
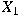 , ,
 , and
this bound is the best possible. , and
this bound is the best possible.
|