Let G
be a finite group,
K a field, and
V a finite-dimensional
KG-module. Write L(V)
for the free Lie algebra on
V; similarly, let M(V)
be the free metabelian Lie algebra. The action
of
G extends naturally to these algebras, so they
become
KG-modules, which are direct sums of
finite-dimensional submodules. This paper
explores whether indecomposable direct summands
of such a
KG-module (for some specific choices of
G,
K and
V) must fall into finitely many isomorphism
classes. Of course this is not a question unless
there exist infinitely many isomorphism classes
of indecomposable
KG-modules (that is,
K has positive characteristic
p and the Sylow
p-subgroups of
K are non-cyclic) and
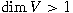 .
.
The first two results show that the
answer is positive for
M(V) when
K is finite and
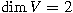 , but negative when
G is the Klein four-group, the characteristic of
K is
2, and
V is the unique
3-dimensional submodule of the regular module
D. In the third result,
G is again the Klein four-group,
K is any field of characteristic
2 with more than
2 elements,
V is any faithful module of dimension
2, and
B is the unique
3-dimensional quotient of
D; the answer is positive for
L(V) if and only if it is positive for each of
L(B),
L(D), and
, but negative when
G is the Klein four-group, the characteristic of
K is
2, and
V is the unique
3-dimensional submodule of the regular module
D. In the third result,
G is again the Klein four-group,
K is any field of characteristic
2 with more than
2 elements,
V is any faithful module of dimension
2, and
B is the unique
3-dimensional quotient of
D; the answer is positive for
L(V) if and only if it is positive for each of
L(B),
L(D), and
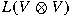 . .
|