J. Aust. Math. Soc.  82 (2007), 297-313

Extending abelian groups to rings

Lynn M. Batten   School of Computing and Mathematics   Deakin University   221 Burwood Highway   Burwood Vic 3125   Australia   lmbatten@deakin.edu.au Robert S. Coulter   Department of Mathematical Sciences   520 Ewing Hall   University of Delaware   Newark, Delaware 19716   USA   coulter@math.udel.edu and Marie Henderson   307/60 Willis Street   Te Aro (Wellington), 6001   New Zealand   marie.henderson@ssc.govt.nz

Abstract

For any abelian group G and any function 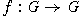we define a commutative binary operation or `multiplication' on G in terms of f. We give necessary and sufficient conditions on f for G to extend to a commutative ring with the new multiplication. In the case where G is an elementary abelian p-group of odd order, we classify those functions which extend G to a ring and show, under an equivalence relation we call weak isomorphism, that there are precisely six distinct classes of rings constructed using this method with additive group the elementary abelian p-group of odd order p2.

Download the article in PDF format (size 168 Kb)

Australian Mathematical Publishing Association Inc. ©  Australian MS